一次関数を得意にするための2つの視点
こんにちは、長谷川です。
来週から後期中間テストが始まりますね!
今回のテーマは「一次関数を得意にするための2つの視点」です。
一次関数は内容、指導時期の2つの観点からとても指導が難しいと感じています。
その2つの視点とは「内容がいきなり難しくなる」「中学2年という多感な反抗期に入る」です。
数学を指導している方は、数学が得意だった方が多いので「一次関数」がなぜ「いきなり内容が難しくなる」のかわからない方が多いです。
ですが、私が27年間に指導してきた経験則から言わせてもらうと「難しい」です。
この「一次関数」から数学が嫌いになった生徒はとても多いです。
また、時期的に反抗期にはいるということも大きな要員です。
大きな要因なのですが、反抗期にはいるのは成長過程で当たり前のことなので、反抗期の生徒にそれ合わせた指導ができないのは「未熟教師」のレッテルを貼られてもしょうがありません。
だってあなたにもあったでしょう。
親とか先生とか大人に対して不信感をいだきますから。
でも、逆に考えるとこれはチャンスにもなるのです。
そんな大人に対して不信感にある子ども。
その子どもに難しいと捉えている「一次関数」をわかりやすく教えることで、その子どもからの信頼感を得ることができるのですから。
私はこの「一次関数」の指導法をめちゃくちゃ研究したので、得意です。
でも、やはり難しいですよ。
気持ちを引き締めて教えましょう!
電子書籍にも書きましたが、
頭が良い人は「一次関数なんて簡単!」と思っているケースが多いです。
何故なら変化の割合が一定だからです。
でもね、普通の子ども達は「一次関数」を難しいと感じているんですよ。
もし、これを読んでいるあなたが生徒に指導している立場であれば、今回お話することを頭の片隅に置くだけで、一次関数の教え方が格段に上手くなります。その結果生徒から感謝されるでしょう。
では「一次関数を得意にするための2つの視点」行ってみましょう!
「値」と「増加量」の違いを認識させること
このブログは子どもを持つ母親とか、子どもたちを指導している方を対象にしていますので、こういう書き方になります。
子どもたちは「値」と「増加量」の区別ができていません。
もちろん中には無意識に出来ていて、なんの苦労もなく認識できてしまう生徒はいます。
ただ、割合で言うと1割から2割でしょうか。
私は神奈川県で最大手の学習塾で指導していきました。
その学習塾は「入会テスト」がありますし、県内の方から「あの塾は優秀な生徒が集まる塾ですよね」と言われる学習塾でもそれくらいの割合です。
ですから、この「値」と「増加量」の違いをここでしっかりと指導したいものです。
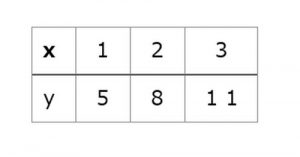
例えばこのような対応表の場合。
対応表に書いてある数値は「値」になります。
ここで子どもたちは一次関数の式をここに書かれている「値」をどうにかして求めようとします。
ところが、一次関数の場合は増加量に注目するので混乱が起きるのです。
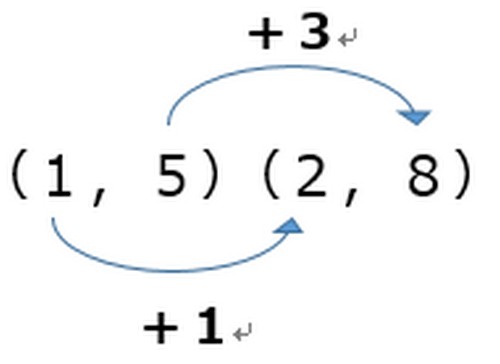
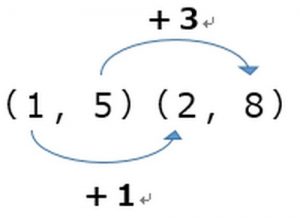
この表の→の上に書いてある数字が増加量です。
要は右の値から左の値の差が「増加量」です。
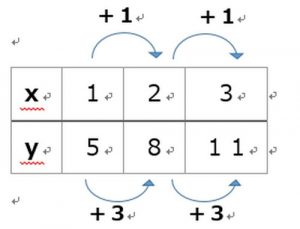
増加量は下の図のようになります。表の上と下に書いてある「+3」と「+1」が増加量です。
この場合、xの増加量を下に、yの増加量を上に書いています。
それは変化の割合がyの増加量/xの増加量になるからです。
視覚的にも生徒の理解に繋がるように書いていきます。
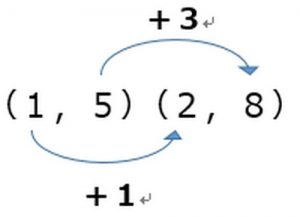
この2つ同じ問題なのですが、子どもたちは同じだとは捉えません。
捉えていたら、凄いことなのですかさず承認・称賛しましょう。
まとめますと、子どもたちが一次関数で悩む1番の理由は「値」と「増加量」の違いを認識できていないことにあります。
そこを認識させることで、かなり正答率は上がるので自信がついてきます。
ただ、1回認識させただけでは足りません。何回も反復演習をすることで、子どもに自信をつけさせましょう。
その過程で、子どもが一次関数の問題で◯が続いたら「凄いね!」って褒めましょう。
何故なら、これはある意味、子どもの頭脳が算数から数学に移行したということなのですから。
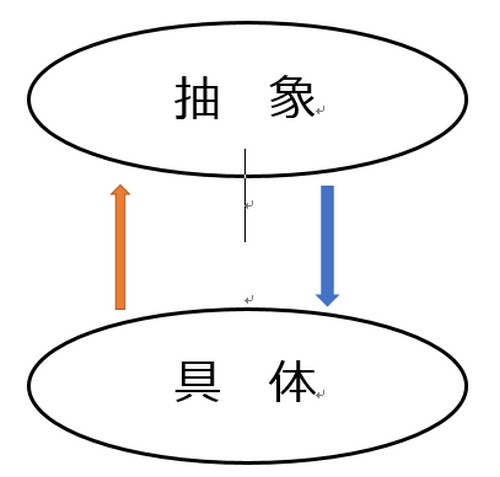
抽象化と具体化
それから最初に伝えた「値」と「増加量」が理解できて問題演習で正答率が上がってきたときに意識したいのは「抽象化」の概念です。
これは少しハードルが高いかもしれません。
しかし、この「具体」↔「抽象」のやりとりが数学の醍醐味であり、社会生活にでたときに1番役立つ内容なのです。
ですから、このブログではそれについても説明していきます。
まずこの図を見て下さい。
先程の「値」と「増加量」をクリアした子どもたちを待ち構える次の障壁はこの「抽象化」にあると言っていいでしょう。
真面目な子どもほど、このパターンはこう解けば良いんだ。次のパターンはこう解くんだ。そして……。
実は、一次関数は次の表に集約されるのです。
全ての問題をこの表と比べあわせて指導してみて下さい。
真面目な子どもで「一次関数」が苦手な生徒は例外なく「そのパターンの多さに嫌気をさしている」のです。
ですから、すべての「一次関数」の問題はこの表に集約されるということを、問題を通して紐付けるだけで、一次関数って実はこれだけなんだと思えて、得意になります。
いわゆる「数学的帰納法」ですね。(たとえですよ。意味違いの反論はしないで下さいね)
このように、たくさんのパターンがあると思っていたのが、実は1つの「原則」に基点しているのだということを理解させることが出来たら、その子どもはものすごい成長を遂げたことになります。
頑張ってくださいね!
もし、指導法や子育てなどで質問や聴きたいことがある場合は下のメールに連絡下さい。
最後の呪文
最後の呪文は「関数はとにかく代入!」です笑
何をして良いのかわからない生徒がいたら、この呪文「とにかく代入!」してみてと伝えましょう。
これである程度の問題が出来るようになる子ども達もいるのは事実です笑
あなたの子どもの成長にお役に立てば嬉しいです。
私の電子書籍「どうしてあなたの子どもはテストの点数が悪いのか?‐子どもがテストで33点アップする魔法の5つの質問」好評発売中です。
タイトルはエグいかもしれません(苦笑)。しかし、なぜテストで点数が取れないのか、またキャリアカウンセリングの視点から子どもを支援する内容、そして私が約2000人を指導してきての体験則を書いています。第4章には子どもの特性を調べるための質問を載せています。これは受験だけではなく、これからの日本を生き抜くための智慧に結びつきます。興味を持たれた方はどうぞ。
———————————————-