今回の内容
円周角の定理は人生の縮図!?-円周角の定理が苦手な子どもへの処方箋
こんにちは、長谷川です。
今日は中学3年生の男の子からの相談です。
「学校で円周角の定理をやっています。 僕、ぜんぜん解けないんです。
先生に聞いても「2倍するか半分にするだけだから簡単だろ!」って言われて笑われてしまいました。
円周角の定理を解くコツみたいなものってあるんでしょうか?もしあるなら教えてください」
はい、もちろん「円周角の定理を解くコツ」はありますよ!
ではいってみましょう!
角だけを見るな!角を作っている弧を探せ!
私は円周角の定理は人生の縮図だとよく生徒に言っています笑。
なぜなら、目の前に答えがあるのに気がつかないからなんですね。
人生の教訓に「全ては自分の中にある」とか「答えは目の前にある」とかあるじゃないですか。
あれに近い感じですね。
詳しくは最後に説明するとして、早速円周角の定理を解くコツを説明しますね。
円周角の定理を解けるようになるには、次の3つのコツがあります。
-
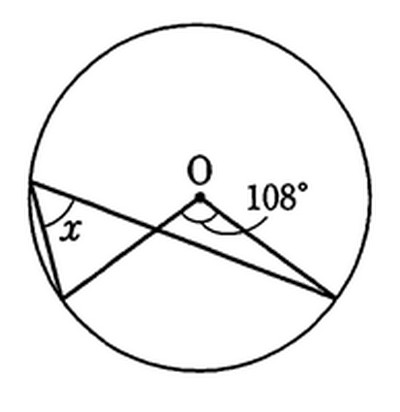
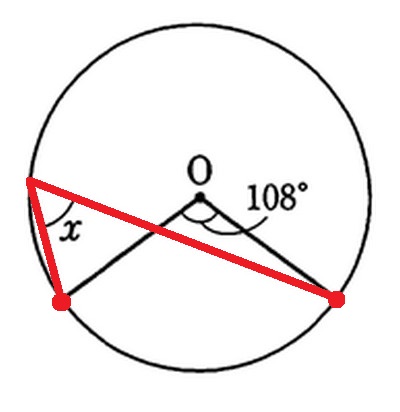
1.求めたい角を作っている孤を確認する
-
2.その孤を中心に中心角、円周角、などを探していく
-
3.二等辺三角形を意識する
では1つずつ説明しますね。
1.求めたい角を作っている孤を確認する
これが1番重要です。円周角の定理が苦手な生徒は「孤」を意識していません。
角ができるためには、そのもとに必ず「孤」があるのです。
この「孤」を意識して練習していけば必ずできるようになりますから、安心してくださいね。
ですから、まず角から孤を見つける練習をします。
そのためには、
1.角を作っている二本の線を角の先端からなぞって、円周にぶつかったら丸くつける。
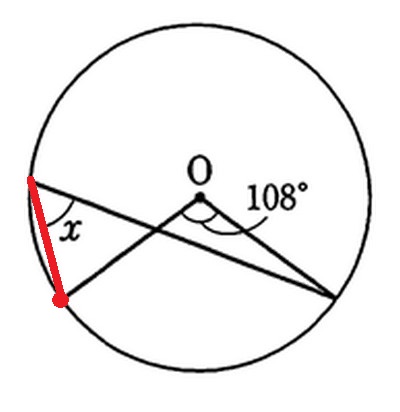
今なぞった、2つの丸の間がその角に対する孤になります。
これ、大人は簡単にできると考えていますが、出来ないですよ。
ですから1回やってわからなくても、辛抱強く指導することが大切です。
ここで、「なんでわかんないの!?」は禁句です。
この言葉でどれだけの子どもたちの勉強の可能性の目を摘んでしまったことやら。
核兵器レベルの「毒の言葉」です。
指導する側は封印しましょう。
また、言われちゃった場合は「今に見てろ!」ってエネルギーに変えましょうね。
話がそれましたが、この角から孤を見つける練習ができたら、もう出来るようになったも同然です。
2.その孤を中心に中心角、円周角、などを探していく
さあ、孤が見つかりました。
次に意識したいのは「その孤が作る他の角をみつけること」です。
中心角、この孤に対する他の円周角はないのか?
その辺りを探って見ます。
ここも演習量を積むことで、できるようになりますから安心してくださいね。
1問1問を大切に解いていきましょう。
3.二等辺三角形を意識する
円は半径の長さが同じなので、二等辺三角形がたくさんできます。
これも当たり前のことなのですが、なかなか気づかないです。
補助線を引くときも、二等辺三角形になるように引いて見るとか。

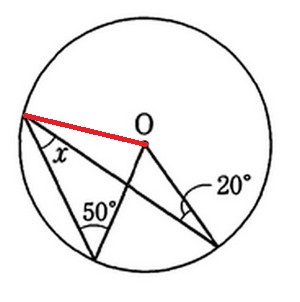
あと、直径に対する円周角は90度になることも意識しましょうね。
問題に直径が引いてあったら、必ず90度はどこだ?って探す癖をつけましょう。
また、直径が書いてあるのに、円周角になっていない場合があります。
こんなとき。
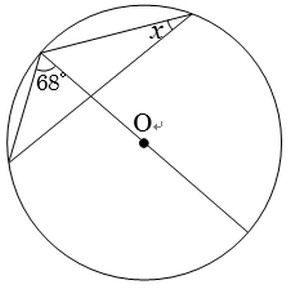
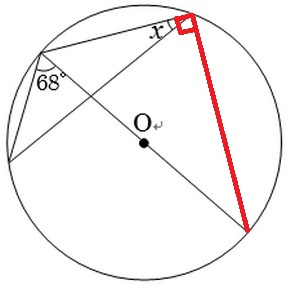
こうやって90°を作っちゃいましょう。
この3つのコツを意識しながら問題を解いていけば円周角の定理は確実に得意になりますよ。
頑張って練習して、慣れてくださいね。
どうして円周角の定理が人生の縮図なのか?
円周角の定理の問題は、補助線を入れなくても解ける問題でも、気がつかないケースが多いです。
まさに答えは目の前にあるのに、気が付いていないわけです。
また、角度を求めるのに、そこではなくて、その角を作っている弧に注目するなんて、目先の現象ではなくて、その原因になっている根本を見つめていくことは、人生でも大切なことなんではないでしょうか?
私はキャリアカウンセラーでもあるので、カウンセリングもしています。
(※国家資格を持っています。2級キャリア・コンサルティング技能士です)
カウンセリングをしていると、クライエントは自分で答えを既に持っているのに、気が付いていない場合が多いです。
傾聴をじっくりやっていくと、クライエント自身がそれに気が付きます。
この過程が興味深くて面白いのです。
クライエントの話したことを要約したり明確化していく中で、クライエントが「あっ!」と気がつく瞬間があります。
この瞬間と円周角の定理で問題を解いていく過程が似ているなあと感じるわけです。
クライエントが自分の中の答えを見つけたら、自ずと主訴は解決していくのです。
そんなわけで「円周角の定理は人生の縮図」というタイトルを付けました。
人生の縮図なのは円周角の定理だけではありませんけどね。
数学というのは、本当に人生に役に立つことが多い科目なのですから。
これに気が付いていない人が多いやら……。
子どもの指導法や子育てなどの悩み質問を受け付けています。お気軽にどうぞ。
Amazon教育部門で1位を獲得! 電子書籍「どうしてあなたの子どもはテストの点数が悪いのか?」
>>2017年3月4日まで、99円でお読みいただけます。
———————————————-
応援よろしくお願いします♪
![]()
にほんブログ村