今回の内容
数学が苦手な子どもが連立方程式の計算を極めるためのコツ
おはようございます、長谷川です。
前回と前々回で連立方程式の計算の攻略の仕方を説明しました。
連立方程式の計算は「加減法」と「代入法」の2つです。
ですから、この2つの解き方をマスターすることができれば良いわけです。
2つだけなのですが、連立方程式の計算を苦手だと思っている子どもたちは「()がついてたり、分数嫌いだし、小数もやだし、沢山有るから連立方程式の計算は嫌い!」となっているケースが多いです。
なので、今日は子どもたちが苦手意識を持っている「()付き、分数や小数、A=B=C型などの連立方程式の計算のコツ」を伝授します。
では、行ってみましょう!
—–
・まずは「加減法」を特訓すること
連立方程式の計算のメインは「加減法」です。
ですから、この「
ミスするポイントは前々回の記事に書いてあります。
連立方程式:加減法でミスを克服する方法【前期期末テスト攻略シリーズ】
次に「代入法」ですが、これは式の形が

になっている時にだけ使います。
どちらを使うかは式の形で認識できるようにします。
y=~や、x=~など形になっている時だけ「代入法」でやるように指導します。
それ以外は「加減法」で計算します。
・連立方程式の計算は2種類なのですが……。
以上のように、連立方程式の計算は2種類だけです。
2種類だけですが、連立方程式の計算に苦手意識を持っている子どもたちは、色んな種類があると思っています。
それは何故かと言うと、()が付いた式や、分数、小数、A=B=Cの形などがあって、それを1つ1つ別々のものだと認識しているからです。
特に真面目な子どもほど、あれもこれもと沢山の種類があると認識しがちです。
沢山あると「こんなにやり方を覚えなくてはいけないんだ」と思ってしまいモチベーションが下がります(苦笑)
ですから「連立方程式の計算は2種類しかないんだよ」ということを認識させると、「なんだ、それならなんとかなる」と感じて苦手意識が薄まります。
では、どうやったら2種類だけと認識させることが出来るのでしょうか?
それは、「()付きも、分数も、小数も、A=B=Cの形も整理整頓するだけ!」ということを問題演習を通して、しっかり感じさせるということです。
・整理整頓のしかた
・1.()付きの式
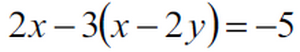
の場合、
分配法則を使って()を外してから同類項をまとめます。
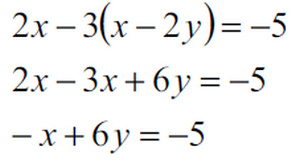
このように整理整頓すればあとはいつもの「加減法」を行うだけです。
・2.分数
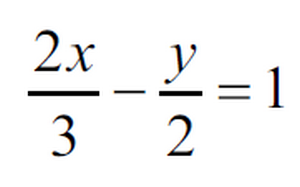
の場合、
両辺に最小公倍数をかけて分母を払います。

分数の場合は分母の数の最小公倍数を両辺にかけて整理整頓すれば、あとはいつもの「加減法」を行うだけです。
・3.小数

の場合、
両辺を10倍します。

少数の場合は、式にある小数の項が小数第1位なら10倍、小数第2位の項なら100倍して整数にして整理整頓します。
・4.A=B=Cの形
この場合、ここから次のように3つの方程式を作ることができます。
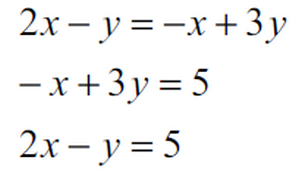
ここから2つの方程式を選ぶわけですが、
コツとして、このように1番右の項が整数の場合は次のように、2つの式とも=整数の形に整理整頓するとのあとの計算が楽です。
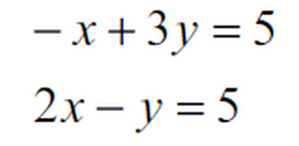
・まとめ
()付きだろうが、分数だろうが、小数だろうが、A=B=Cだろうが、
結局は
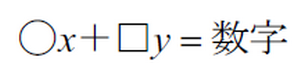
の形に整理整頓するだけです。
もちろん、子どもたちそれぞれ個人差がありますから、上の4つパターンのうち特に苦手なものは水道方式のように練習が必要です。
でも、結局は「整理整頓するだけ」という認識を持つだけでモチベーションは変わります。
今回の夏期講習でも、このことを子どもたちに指導してきました。
もちろん伝え方は大切です。
私は今回の夏期講習でも、分数や小数を見てやる気が無くなってる生徒には、
「A君は、もう加減法はバッチリ出来るじゃん。
A君は分数好き?」
A君:「大っ嫌い」
(ほぼ100%に近い確率で「嫌い」と返ってきます(笑))
私:「方程式は両辺に同じ数をかけることができるよね?
だから、実はこの分数の方程式も整数に直せるんだよ。
整数に直せたら、A君は加減法は出来るわけだから、大丈夫だよね?」
A君:「整数の加減法なら、出来ます」
「うん、だから今日は整数に直す、直し方さえ出来るようになれば良いんだよ!」
A君:「整数に直す直し方だけで良いんだ!じゃあやってみます」
これを()付き、分数、小数、A=B=Cの形のときにも同じことが繰り返すだけです。
ポイントは「整理整頓」であり、「いつもの形に直すだけ」ということに意識を向けさせます。
これはある意味「抽象化」するということです。
この場合なら「沢山の種類の方程式があるけど、結局は整理整頓して整数にして加減法で解けば良いんだ!」と認識させることが、とても大切なのです。
ただ、計算ができればいいとかで終わってしまったら、もったいないです。
「具体」から「抽象」へ導くことを子どもたちに教えることの方が、社会に出てからとっても役に立つのです。
この感覚を教えることが、数学を教えるある意味醍醐味の一つなんですね。
イメージはこれです。
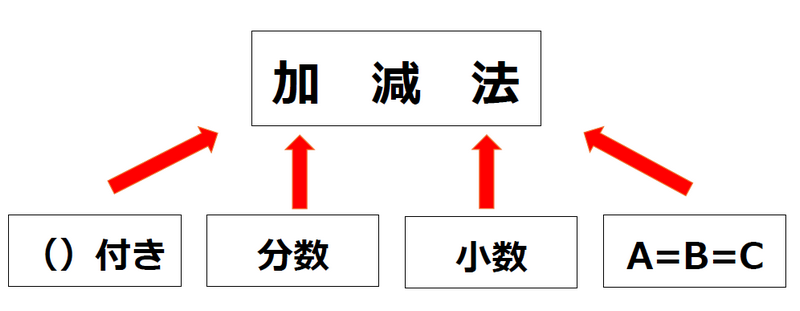
「()付き」「分数」「小数」「A=B=C」は「整理整頓」というフィルターを通して「加減法」という1つのものに「抽象化」されるのです。
私は子どもたちにもこの「抽象化」の大切さを話しています。
何故なら、私自身が社会に出てからこの「抽象化」の大切さを痛感しているからです(苦笑)
意外にも子どもたちは難しい顔をしないで、寧ろ「へぇー、数学って凄いんだ!」って興味津々の顔つきで聞いてますよ。
なので、「整理整頓して、整数に直す!」を合言葉に、連立方程式の計算を得意にしてしまいましょう!
連立方程式の計算をきちんとおこなうには「正負の数」の計算がしっかり身についていなければなりません。「正負の数」について勉強し直したい方はこちらをご覧ください。
▷ 自尊心を育む数学講座【The Sky Is The Limit!】①「正負の数」の詳細はこちら
お子さんの勉強に対する悩み相談もやってます。
▷ 勉強が嫌いな子どもへの処方箋
——————-
応援よろしくお願いします♪
![]()
にほんブログ村